Tip 1: Sådan konverteres tal til binær notation
Tip 1: Sådan konverteres tal til binær notation
Ud over det sædvanlige decimalsystem radix, der er andre systemer. De mest almindelige af dem er binære, oktale, hexadecimale. Disse systemer anvendes primært i computerteknologi. At oversætte tal fra et system radix i den anden er der enkle operationer. Overvej hvordan man oversætter antal i binær systemet radix fra andre systemer.

instruktion
1
At oversætte oktal antal i binær systemet Det er nødvendigt at præsentere hver af sine tal i formularentriad med binære cifre. For eksempel nedbrydes det oktale nummer 765 i triader som følger: 7 = 111, 6 = 110, 5 = 101. Resultatet er et binært tal 111110101.
2
At oversætte hexadecimal antal i binær systemet radix Det er nødvendigt at præsentere hver af sine tal i formularentetrads med binære cifre. For eksempel dekomponeres det hexadecimale nummer 967 i tetrader som følger: 9 = 1001, 6 = 0110, 7 = 0111. Resultatet er et binært tal på 100101100111.
3
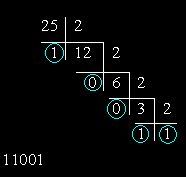
At konvertere decimaltalet til binært systemet radix, er det nødvendigt at opdele det konsekvent i to, hver gang der skrives resultatet som helhed antal og resten. Opdelingen skal fortsættes, indtil der er et tal lig med en. Det endelige tal opnås ved sekventielt registrering af resultatet af den sidste division og resuminaterne af alle divisioner i omvendt rækkefølge. Som et eksempel viser figuren fremgangsmåden til oversættelse af decimaltegnet antal 25 til binær systemet radix. Den på hinanden følgende deling i to giver følgende sekvens af rester: 10011. Udvidelse af det tværtimod, vi får det nødvendige nummer.
Tip 2: Sådan konverteres til binær
Komponenterne i elektroniske maskiner, hvortilder er også computere, der er kun to skelne tilstande: der er en strøm, og der er ingen strøm. De betegnes henholdsvis "1" og "0". Da der kun er to sådanne stater, kan mange processer og operationer i elektronik beskrives ved hjælp af binære tal.

instruktion
1
For at oversætte en brøkdel decimalnummer i binært tal system, følg følgende algoritme. Overvej operationen af algoritmen ved hjælp af eksemplet på nummer 235.62. For det første oversættes heltaldelen af tallet.
2
Del decimaltalet med to tilvi får en udelelig rest. Ved hvert divisionstrin får vi resten 1 (hvis udbytteantalet er ulige) eller 0 (hvis udbyttet er deleligt med to uden rest). Alle disse rester skal tages i betragtning. Det sidste delresultat, der opnås som følge af en sådan trindeling, vil altid være en enhed. Vi skriver den sidste enhed i det højeste ciffer i det krævede binære tal, og de opnåede rester i processen skrives ned for denne enhed i omvendt rækkefølge. Her skal du være forsigtig og ikke springe over nuller. Så vil nummeret på 235 i den binære kode svare til nummeret 11101011.

3
Oversæt nu til binært tal systemden delvise del af decimaltalet. For at gøre dette multiplicerer vi den brøkdel af tallet med 2 og retter heltalsdelen af de opnåede tal. Disse heltalsdele tilføjes til det nummer, der blev opnået i det foregående trin efter det binære punkt i den direkte rækkefølge. Derefter svarer decimaltraktionsnummeret 235,62 til den binære fraktion 11101011.100111.

Tip 3: Sådan oversætter du talesystemet
I informationsteknologi bruges i stedet for det sædvanlige decimaltalsystem ofte binært, da computerens arbejde er bygget på det.

instruktion
1
Hovedoperationerne er kun to: oversættelse fra decimaltal til en anden (binær, oktal osv.) og omvendt. Navnet på hvert talesystem kommer fra dets base - antallet af elementer i det (binært - 2, decimal - 10). I basisnotationssystemer med en base større end 10 er det almindeligt at bruge bogstaverne i det latinske alfabet (A-10, B-11 osv.) Som erstatning for tocifrede tal.
2
Lad os overveje operationerne ved hjælp af eksemplet på et binært systemnummerering, som den mest almindelige. For alle andre systemer gælder de samme regler og metoder for udskiftning af base 2 med den tilsvarende. Så vi har et nummer i det binære talesystem bestående af flere cifre. Vi skriver det i form af summen af produkterne af sine cifre multipliceret med 2. Herefter arrangerer vi alle kræfter fra højre til venstre fra 0. Vi opsummerer. Det resulterende nummer er det du søger. Eksempel. 1011 = 2 * 2 + 11.
3
Overvej nu omvendt drift.Lad der få et tal i decimalsystemet. Vi fordeler det ved en kolonne på basis af det talesystem, som vi vil oversætte det til (i vores tilfælde er det 2). Opdelingen fortsætter helt til sidst, indtil den private bliver mindre end jorden. Derefter begynder vi med det sidste at skrive ned alle rester i linjen. Dette er det ønskede nummer. Eksempel 11/2 = 5 resten er 1, 5/2 = 2, resten er 1, 2/2 = 1 resten er 0 => 1011. Et andet eksempel er vist på billedet. For andre baser er operationerne ens. Glem ikke at erstatte tallene, begyndende med 10, i de tilsvarende talesystemer i latinske bogstaver! Ellers vil det resulterende tal blive læst forkert, fordi "10" og "1" "0" er helt forskellige ting! Basen af talesystemet, hvor tallet er repræsenteret, er angivet i form af et indeks nederst i tallets højre ciffer.

Tip 4: Sådan oversætter du tal fra et system til et andet
I kontosystemet, som vi bruger hverdag, ti tal - fra nul til ni. Derfor kaldes det en decimal. Men i tekniske beregninger, især de relaterede til computere, andre systemet, især binær og hexadecimal. Så du skal kunne oversætte antal fra en systemet nummerering i en anden.

Du skal bruge
- - et stykke papir
- - en blyant eller pen
- - lommeregner.
instruktion
1
Det binære system er det enkleste. Der er kun to cifre i det - nul og en. Hvert ciffer af binære antal, der begynder med slutningen, svarer til kraften af to. To til nul grader er lig med en, i de første to, i den anden - fire, i den tredje - otte, og så videre.
2
Antag at du får et binært tal på 1010110. Enheder i den står på den anden, tredje, femte og syvende fra enden af feltet. Derfor er dette tal i decimalsystemet lig med 2 ^ 1 + 2 ^ 2 + 2 ^ 4 + 2 ^ 6 = 2 + 4 + 16 + 64 = 86.
3
Det omvendte problem er oversættelsen af decimaltalet antal i det binære system. Antag, at du har en række 57. For at få sin binære repræsentation, er du nødt til konsekvent at dividere dette tal med 2 og optage resten af divisionen. Den binære tal vil blive bygget fra slutningen til nachalu.Pervy skridt vil give dig det sidste ciffer: 57/2 = 28 (rest 1) Så, du kommer til slutningen af den anden: 28/2 = 14 (resten 0) Længere trin: 14/2 = 7 (resten 0) 7/2 = 3 (rest 1) 3/2 = 1 (rest 1) 1/2 = 0 (rest 1) .Denne sidste trin, fordi resultatet af divisionen er nul. Som et resultat, du har modtaget binært tal 111001.Proverte korrekte svar: 111001 = 2 ^ 0 + 2 ^ 3 + 2 ^ 4 + 2 ^ 5 = 1 + 8 + 16 + 32 = 57.
4
Det andet talesystem, der anvendes icomputer problemer - hexadecimal. Det er ikke ti, men seksten tal. For ikke at oprette nye symboler, de første ti cifre i hexadecimal systemet betegnes med sædvanlige cifre, og de resterende seks - i latinske bogstaver: A, B, C, D, E, F. decimaltegn svarer de antalm fra 10 til 15. For at undgå forvirring er et tegn på # eller 0x foran et nummer skrevet på et hexadecimalt system.
5
At konvertere et tal fra hexadecimal systemet i decimaltal skal du multiplicere hvert af dens nummer vedden tilsvarende grad af seksten og tilføj resultaterne. For eksempel er tallet # 11A i decimaltallet 10 * (16 ^ 0) + 1 * (16 ^ 1) + 1 * (16 ^ 2) = 10 + 16 + 256 = 282.
6
Omvendt oversættelse fra decimal systemet i hexadecimalt sker ved samme metoderester, som i binær. F.eks. Tag nummeret 10.000. Del konsekvent med 16 og optag resten, så får du: 10000/16 = 625 (balance 0) .625 / 16 = 39 (saldo 1) .39 / 16 = 2 (saldo 7) .2 / 16 = 0 (balance 2). Resultatet af beregningen er hexadecimalt nummer # 2710. Kontroller svarets rigtighed: # 2710 = 1 * (16 ^ 1) + 7 * (16 ^ 2) + 2 * (16 ^ 3) = 16 + 1792 + 8192 = 10000.
7
oversætte antal fra hexadecimal systemet Nummereringen i binær er meget enklere. Nummer 16 er en effekt på to: 16 = 2 ^ 4. Derfor kan hver hexadecimal tal skrives som et firecifret binært tal. Hvis du har et binært tal opnås mindre end fire cifre, føje til toppen af nuli.Naprimer, # 1F7E = (0001) (1111) (0111) (1110) = 1111101111110.Proverte Korrekt svar: Både antal i decimaltallet er 8062.
8
For den omvendte oversættelse skal du dele det binæredet antal grupper af fire numre, der starter fra enden, og enhver sådan gruppe erstattet hexadecimal tsifroy.Naprimer, 11000110101001 omdannet til (0011) (0001) (1010) (1001), som i hexadecimal notation giver # 31A9. Korrektheden af svaret bekræftes af en oversættelse i decimaltegnet: begge antal er lig med 12713.
Tip 5: Sådan konverteres et nummer til binært
På grund af den begrænsede brug af symboler er det binære system mest bekvemt til brug i computere og andre digitale enheder. Symbolerne er kun to: 1 og 0, så dette systemet gælder i registret.

instruktion
1
Det binære system er positionelt,dvs. Positionen for hvert ciffer i nummeret svarer til et bestemt ciffer, hvilket er lig med to i den tilsvarende grad. Graden starter fra nul og øges, når du flytter fra højre til venstre. For eksempel antal 101 er lig med 1 * 2 ^ 0 + 0 * 2 ^ 1 + 1 * 2 ^ 2 = 5.
2
At oversætte antal fra ethvert andet nummereringssystem til binære,du kan bruge to metoder: sekventiel division med 2 eller ved at oversætte hvert ciffer af et tal i en tabel i de tilsvarende firdobler af binære tal.
3
En bred fordeling blandt positionssystemerogså bruge oktale, hexadecimale og decimaltal systemer. Og hvis for de to første er den anden metode mere anvendelig, så gælder begge for oversættelse fra decimalsystemet.
4
Overvej konverteringen af et decimaltal til et binært tal systemet ved en metode til successiv division med 2. At oversætte decimaltallet antal 25 i binær kode, skal du dele det med 2 tilså længe det ikke forbliver 0. Resterne opnået ved hvert opdelingstrin skrives til rækken fra højre til venstre, efter at der er skrevet cifferet til den sidste resterende, vil dette være det endelige binære antal. Så: 25/2 = 12, 1 i resten => 1; 12/2 = 6, resten er ikke til stede => 0; 6/2 = 3, resten er ikke til stede => 0; 3/2 = 1, 1 i resten => 1;? = 0, 1 i resten => 1. Oversættelsen af oversættelsen er som følger: 25_10 = 11001_2.
5
Octal og hexadecimale talkonverteres til binær kode ved at erstatte hvert ciffer med de tilsvarende fire kode symboler i det binære system. Oversættelsestabellen er som følger: 0 = 0000 1 = 0001, 2 = 0010 3 = 0011, 4 = 0100 5 = 0101 6 = 0110 7 = 0111 8 = 1000 9 = 1001, A = 1010, B = 1011, C = 1100, D = 1101, E = 1110, F = 1111.Naprimer: 61_8 => [6 = 0110] [1 = 0001] => 01100001_2; 9EF_16 => [9 = 1001] [E = 1110] [F = 1111] => 100111101111_2.
Tip 6: Hvad er talesystemerne
Nummersystemet er en måde at skrive numre på nårhjælpe specielle tegn, det vil sige repræsentationen af nummeret skriftligt. Nummersystemet giver nummeret en vis standard repræsentation. Afhængigt af æra og anvendelsesområde eksisterede der og eksisterer mange talesystemer.

instruktion
1
De eksisterende talesystemer kan opdeles i tre hovedtyper: positions-, blandet og ikke-positionelt.
2
I positionssystemer, tegnet eller nummeretkan have en anden værdi afhængigt af positionen. Systemet bestemmes af antallet af symboler, der anvendes i det. Det mest populære og almindeligt anvendte decimalsystem. I det er alle tal repræsenteret af en bestemt sekvens på ti cifre fra 0 til 9.
3
Arbejdet i al digital teknologi er baseret på et binært tal system. Den bruger kun to tegn: 1 og 0. Alle store tal repræsenteres af forskellige kombinationer af disse tal.
4
I visse beregninger er den ternære ogoktal nummer system. Kendt er også den såkaldte tæller med snesevis eller det duodecimale talesystem. I datalogi og programmering er hexadecimal notation meget populær, da det giver dig mulighed for at skrive et maskinord - en dataenhed, når du programmerer.
5
Blandede nummersystemer ligner positionelle. I blandede systemer er tal repræsenteret af en stigende sekvens. Forholdet mellem medlemmer af denne sekvens kan være helt anderledes.
6
Så til det blandede system af nummerering kan tilskrivesFibonacci sekvens, hvert antal som er lig med summen af de to tidligere serier af numre, der starter med 1. Dvs. sekvensen er 1, 1 (0 + 1) 2 (1 + 1) 3 (1 + 2), 5 (2+ 3) og så videre.
7
Hvis du repræsenterer en time record i formatetdag-time-sekund, så er dette også et blandet nummer system. Enhver af betingelserne i en sekvens kan udtrykkes i form af et minimum, det vil sige om et sekund. Et hyppigt anvendt eksempel på et blandet system i matematik er det faktorialnummer system, der repræsenteres af en række factorials.
8
I ikke-position nummer systemer, værdienSystemets symbol er fast og afhænger ikke af dets position. Disse systemer er ekstremt sjældne, og de er også matematisk komplekse. Typiske eksempler på sådanne systemer er: Stern-Brocko-nummersystemet, det resterende klassesystem, binomialtalsystemet.
9
På forskellige tidspunkter anvendte forskellige folksæt af talesystemer. For eksempel var det romerske talesystem, der var kendt i dag, meget populært. I den for at skrive tal blev de latinske bogstaver V-5, X-10, L-50, C-100, D-500, M-1000 anvendt.
10
Også der var kendt sådanne nummereringssystemer som single, quinary, babylonian, hebraisk, alfabetisk, oldtidens egyptiske, maya, kipu, inca.







